对比线性结构和树型结构:
同:①线:第一个数据元素无前驱;树:根节点无前驱
②线:最后一个数据元素无后继;树:多个叶子结点无后继
异:线:其他数据元素:一个前驱,一个后继;树:其他数据元素:一个前驱,多个后继
概念:1.树结构是一类重要的非线性数据结构;2.树是以分支关系定义的层次结构;
3.树的应用:①操作系统:表示文件目录的组织结构;②编译系统:表示源程序的语法结构;③数据库系统:信息的重要组织形式
4.树:是n(n>=0)个结点的有限集 ①n==0:空树; ②非空树:(1)有且仅有一个称为根的结点;(2)除根节点以外其余结点可分为m(m>0)个互不相交的有限集T1,T2,T3..Tm 每个集合本身又是一棵树,叫做根的子树
5.树的基本术语:①结点;②结点的度:结点的子树个数 ;③树的度:树内各节点度的最大值;④树的深度:树中结点的最大层次
⑤叶子(终端)结点:度为0的结点;⑥非终端结点:度不为0,除根节点外的非终端结点 叫 内部结点 ;⑦双亲和孩子;⑧兄弟;⑨祖先;⑩子孙
6.二叉树:
重点研究二叉树的原因:
(1)二叉树的结构最简单,规律性最强;(2)所有树都能转为唯一对应的二叉树,不失一般性;(3)普通树转化为二叉树后,运算容易实现
①特点:(1)每个节点至多只有两棵子树;(2)子树有左右之分,其次序不可颠倒
②性质:(1)在二叉树第i层上至多有2^(i-1)个结点(i>=1;(2)深度为k的二叉树至多有2^k-1个结点(k>=1) ;
深度为h的满m叉树的第k层有( )个结点。(1=<k=<h)
A.mk-1 B.mk-1 C.mh-1 D.mh-1


答案:A解释:深度为h的满m叉树共有mh-1个结点,第k层有mk-1个结点。
(3)对于任何一课二叉树,如果终端结点数为n0,度为2的结点数为n2,则n0=n2+1
经典题型:
1.在一棵度为4的树T中,若有20个度为4的结点,10个度为3的结点,1个度为2的结点,10个度为1的结点,则树T的叶结点个数是:


82设N为总的节点数!总的入度=20*4+10*3+1*2+10*1=122=N-1,所以N=123.而N又=20+10+1+10+n(n为度为0的点,即叶子)即n=82
2.一棵完全二叉树上有1001个结点,其中叶子结点的个数是( )。
A.250 B. 500 C.254 D.501


答案:D解释:设度为0结点(叶子结点)个数为A,度为1的结点个数为B,度为2的结点个数为C,有A=C+1,A+B+C=1001,可得2C+B=1000,由完全二叉树的性质可得B=0或1,又因为C为整数,所以B=0,C=500,A=501,即有501个叶子结点。
1.顺序存储结构 2.链式存储结构
#define MAXSIZE 100 typedef struct BiTNode{
typedef TElemType SqBiTree[MAXSIZE]; TElemType data;//结点指针域
SqBiTree bt; struct BiTNode *lchild,*rchild;//左右孩子 }BiTNode,*BiTree
满二叉树:①特点:深度为k,且具有2^k-1个结点的二叉树;②每一层上的结点数都是最大结点数,即每一层i的结点数都具有最大值2^(i-1);
③完全二叉树:①特点:(1)叶子结点只可能在层次最大的两层出现;(2)对任一结点,若其右分支下子孙最大层为l,则其左分支下子孙的最大层次必为l或者l+1
②性质:(1)具有n个结点的完全二叉树的深度为log2-n(向下取整)+1;
一个具有1025个结点的二叉树的高h为( )。
A.11 B.10 C.11至1025之间 D.10至1024之间


答案:C解释:若每层仅有一个结点,则树高h为1025;且其最小树高为 ëlog21025û + 1=11,即h在11至1025之间。
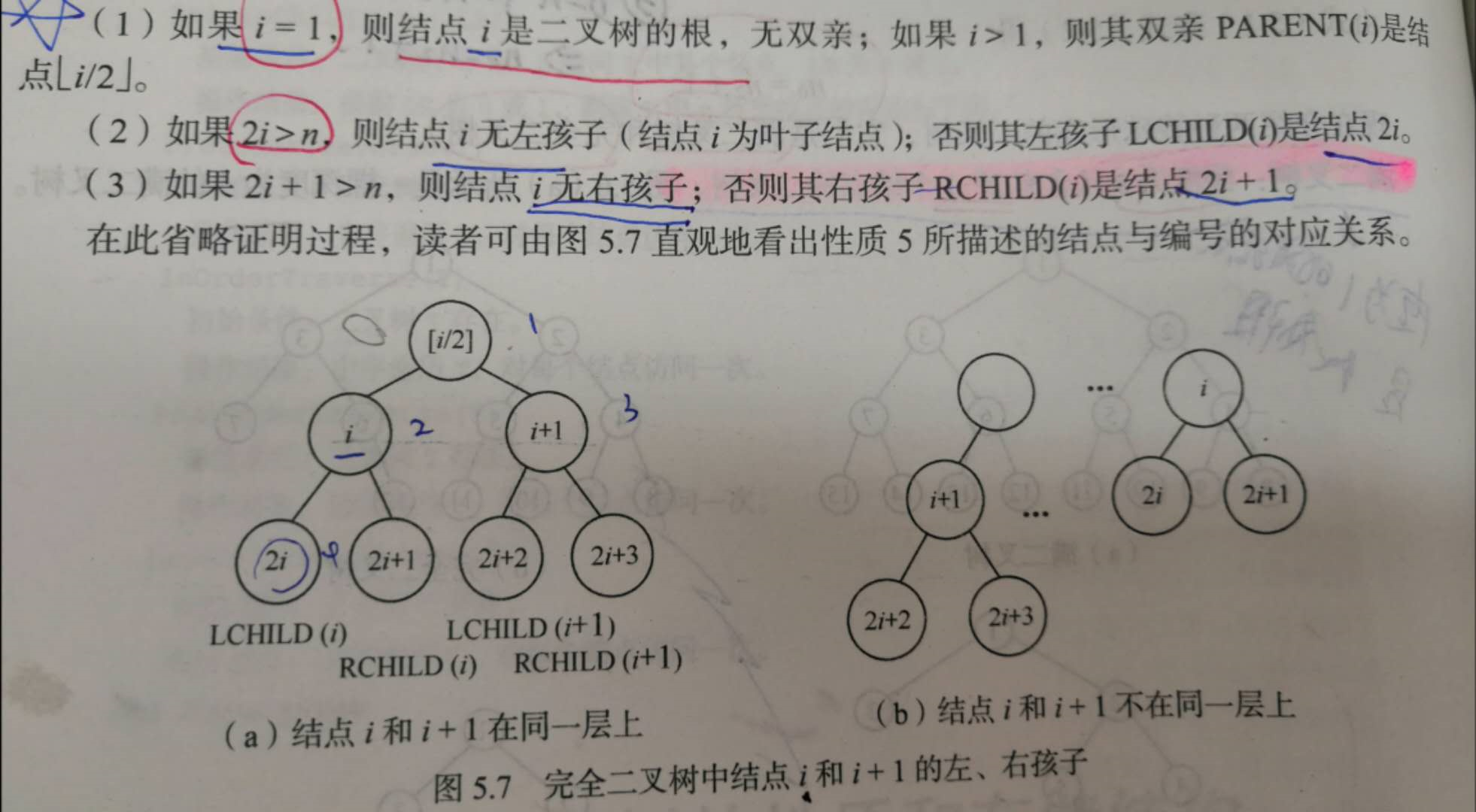
(2)